The first thing I am proposing is a change to z-scores. Z-scores, for those short one introductory statistics course, are measures of relativity to the mean. The formula to calculate a z-score is
So, a z-score measures how many standard deviations you are away from the mean. (Positive z-scores indicate a score above the mean, negative z-scores below.) One benefit of using z-scores is that it takes into account the actual grade, instead of the letter representation. In a class where anywhere from an 85 to a 100% gets you an A, the low end of the range is just as good as the perfect grade - each will get you a 4.0. If you use z-scores, however, it will show that the student with a 100 performed better than the student with the 85.
So that takes care of relativity within each class, but what about relativity between classes? As I mentioned before, not all classes are created equal. An A in Calc III is more impressive than an A in Calc I or II. I don't have an exact measure to represent the strength of each class, but what schools could do is rank each class on how hard it is to get an A, how hard it is to get a B, etc.
If you were to take the average of all of the GPAs in a school, you could say that the average incoming student will have that GPA after four years (making note to fluctuations in GPA over time). That student could take easier courses, do well in them, and have an above-average GPA. Which is a misrepresentation of the student's true abilities. Z-scores, taking into account relativity within and between classes, would indicate how well the average student would do in the average class. It's a lot harder to finagle your way to a higher score when 25 people are involved in the calculation, instead of just one.
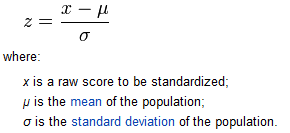
No comments:
Post a Comment